Calorimetry Background
Adapted from Material used at the University of Kansas by J. M. McCormick
Last Update: December 19, 2012
Theoretical Background
Tabulated values of reaction enthalpies are always quoted at some fixed temperature. Since we can write any reaction as Eqn. 1, where R(T) and P(T) are the reactants and products, respectively, at a constant temperature, T, the reaction enthalpy may be written as ΔrH(T) to emphasize that it applies when both the reactants and the products have the same temperature.
| R(T) → P(T) | (1) |
But what is actually measured in an adiabatic calorimeter under constant pressure is Eqn. 2, where K represents the calorimeter and T1 and T2 are the initial and final temperatures, respectively. Since this is an adiabatic process, the change in enthalpy for Eqn. 2 is zero (ΔH2 = 0).
|
R(T1) + K(T1) → P(T2) + K(T2) |
(2) |
There are several ways that the reaction actually taking place in the calorimeter (Eqn. 2) could be imagined as occurring. For example, we could conceive of an initial step where the chemical reaction occurs at constant temperatureT1, followed be a second step in which the heat released, or absorbed, in the first step raises, or lowers, the temperature of the products and the calorimeter to T2, as shown in Eqn.s 3a and 3b.
|
R(T1) → P(T1) |
(3a) |
|
P(T1) + K(T1) → P(T2) + K(T2) |
(3b) |
An alternate approach, and one that is more useful, is to consider a model where the reactants are heated, or cooled, from T1 to T2 in an initial step which is then followed by the chemical reaction which occurs at temperature T2. This model is shown as Eqn.s 4a and 4b.
|
R(T1) + K(T1) → R(T2) + K(T2) |
(4a) | |
|
R(T2) → P(T2) |
(4b) |
Clearly, the sum of Eqn. 4a and Eqn. 4b is Eqn. 2, and as a result:
| ΔH4a + ΔH4b = ΔH2 | (5) |
We can then evaluate the enthalpy change for Eqn. 1 at T = T2 by noting that ΔH4b is simply ΔrH(T2). Since ΔH2 = 0, Eqn. 5 can be rewritten as
|
ΔrH(T2) = -ΔH4a |
(6) |
The process described by Eqn. 4a is a simple heating or cooling process, and thus the enthalpy change for this process can, for small ΔT values, be written as Eqn. 7, where ΔT = T2 – T1 and Cp(R + K) is the heat capacity at constant pressure of the reactants, R, and the calorimeter, K.
|
ΔH4a = Cp(R + K)ΔT |
(7) |
Furthermore, we can write explicitly Cp(R + K) for the case of two reactants, A and B, as
|
Cp(R + K) = mACp(A) + mBCp(B) + Cp(K) |
(8) |
Here mA and mB are the masses of A and B, in grams, and Cp(A) and Cp(B) are the heat capacities of the reactants A and B, respectively, in J·K-1·g-1, or other convenient units. The heat capacities Cp(R + K) and Cp(K) are in J·K-1.1 The heat capacity of the empty calorimeter, Cp(K), is constant from run to run, while the other terms in Eqn. 8 depend on the type and amount of the reactants. In general, the first two terms on the right-hand side of Eqn. 8 can be computed from known data and Cp(K) can be obtained by calibration of the calorimeter. Thus, Eqn. 9 (obtained by substitution of Eqn. 8 into Eqn. 7 and the resulting equation substituted into Eqn. 6) can be evaluated and ΔrH(T2) determined.
|
ΔrH(T2) = -(mACp(A) + mBCp(B) + Cp(K))ΔT |
(9) |
Practical Considerations
What has been described above it the ideal calorimetry experiment where the reactants are at T1 initially and there is a chemical reaction that instantaneously changes the temperature to T2. Unfortunately, this seldom happens in real life where even very good calorimeters slowly leak heat over time, as shown on an exaggerated scale in Fig. 1. Although the scale is exaggerated in Fig. 1 to emphasize the decreasing temperature due to heat loss from the calorimeter both before and after the reaction occurred, the process by which we account for these changes is straightforward. We fit the data before and after the reaction occurs to a straight line and then extrapolate the lines back to the time at which the reaction was initiated. Each equation is solved for the temperature, T, at that time and from these two temperatures, ΔT can then be calculated.
If the reaction is not fast, one may observe curvature in the data after the reaction is initiated but before the linear decrease in temperature with time begins. This sort of behavior is observed between about 3.5 and 4 min in Fig. 1, and is most often seen in experiments to measure the enthalpy of solution of a solid when the solid is not finely ground. Curvature such as this can lead to error in ΔT, depending on what points are included in the regression analysis. Fitting programs (such as Vernier’s LoggerPro) that have interactive linear regression take some of the guess work out of determining which points to include, as the goodness of fit parameter for the best-fit line will become worse as points in the curved region are selected. However, care should always be taken in selecting the points and the uncertainty must be propagated through to the final result.
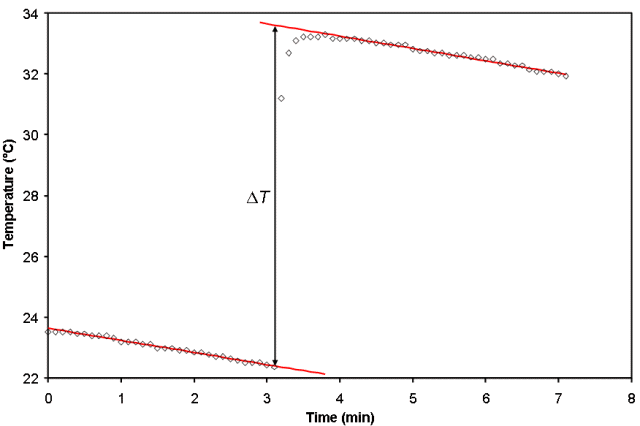Figure 1. A graph of temperature as a function of time for a non-ideal calorimeter.
Notes
1. Our convention in Eqn. 8 is that for a pure liquid or pure solid reactant, mA and Cp(A) refer to the pure liquid or solid. For a reactant in solution, mA and Cp(A) would refer to the solution, not the solute. For example, if reactant A were 100 ml of 0.1 M HCl, then mA would be the weight of the solution and the heat capacity would be per gram of this solution. 2. The problem of fitting temperature as a function of time data in a calorimetry experiment is also discussed in to the CHEM 130 calorimetry lab, which you may refer to for additional information.