Introduction to Statistics in Chemistry1
Authors: B. D. Lamp, D. L. McCurdy, V. M. Pultz and J. M. McCormick*
Introduction
“Figures often beguile me, particularly when I have the arranging of them myself; in which case the remark attributed to Disraeli would often apply with justice and force: ‘There are three kinds of lies: lies, damned lies and statistics.’” -Mark Twain
Twain’s dyspeptic view of figures and statistics notwithstanding, the predictive power of science derives from quantifying (placing numbers on) physical properties, and then writing mathematical equations to describe the Universe’s behavior (laws and theories).2 In this way, we can predict the outcomes of experiments that we have not yet done, and thereby test our models of the Universe. Once we have actually done the experiments we will also need a mathematical way of assessing the reliability of our results. It is in the latter application that scientists rely on statistics. The following is intended to provide you with a basic, working understanding of statistical analysis in chemistry. For a more complete treatment of statistics you will want to take STATS 190/2903 and CHEM 222.4,5
There are three terms that are used by scientists in relation to their data’s reliability. They are accuracy, precision and error. Accuracy is how close a measured value is to the true, or accepted, value, while precision is how carefully a single measurement was made or how reproducible measurements in a series are. The terms accuracy and precision are not synonymous, but they are related, as we will see. Error is anything that lessens a measurement’s accuracy or its precision.
To beginning science students the scientific meaning of “error” is very confusing, because it does not exactly match the common usage. In everyday usage “error” means a mistake, but in science an “error” is anything that contributes to a measured value being different than the “true” value. The term “error” in science is synonymous with “mistake” when we speak of gross errors (also known as illegitimate errors). Gross errors are easy to deal with, once they are found. Some gross errors are correctable (a mistake in a calculation, for example), while some are not (using the wrong amount of a reactant in a chemical reaction). When met with uncorrectable gross errors, it is usually best to discard that result and start again.
The other types of “errors” that are encountered in science might be better referred to as uncertainties. They are not necessarily mistakes, but they place limits on our ability to be perfectly quantitative in our measurements because they result from the extension of a measurement tool to its maximum limits. These uncertainties fall into two groups:systematic errors (or determinate errors) and random errors (or indeterminate errors).
A systematic error is a non-random bias in the data and its greatest impact is on a measurement’s accuracy. A systematic error can be recognized from multiple measurements of the same quantity, if the true value is known. For example, if you made three measurements of copper’s density and got values of 9.54, 9.55 and 9.56 g/cm3, you would not be able to determine whether a systematic error was present, unless you knew that the accepted value of copper’s density is 8.96 g/cm3. You might then suspect a systematic error because all of the measured values are consistently too high (although the closeness of the data to each other implies some level of confidence). Often in science one needs to assess the accuracy of a measurement without prior knowledge of the true value. In this case the same experiment is performed with samples where the quantity to be measured is known. These standards, or knowns, can reveal systematic errors in a procedure before measurements are made on unknowns, and give the experimenter confidence that they are getting accurate results.
The last type of uncertainty is random error. As the name suggests, these uncertainties arise from random events that are not necessarily under the control of the experimentalist. Random errors can be thought of as background noise. The noise restricts our ability to make an exact measurement by limiting the precision of the measurement. Because indeterminate errors are random, they may be treated statistically.
Accuracy can be expressed as a percent error, defined by Eqn. 1, if the true value is known. Note that the percent error has a sign associated with it (‘+’ if the measured value is larger than the true value, and ‘-’ if it is less than the true value). Using the copper density data
| |
(1) |
from above and Eqn. 1, we can calculate a percent error for each data point of approximately +6.5%. This suggests the presence of a systematic error because, if there were no systematic error, we would expect the percent error for each member of the data set to be very small and that there would be both positive and negative values. When the true value is not known, no conclusion about accuracy may be made using a percent error. In this case, standards must be run or other statistical methods based on the precision can be used. However, the latter can be used only to assess the accuracy of a group of measurements.
In the absence of systematic errors, the average, , of a set of measurements (Eqn. 2) should approximate the true value, as the number of measurements, N, becomes very large (i. e., there are many individual data points, xi). But if a systematic error is present, then making more
| |
(2) |
measurements will not make the average approach the true value (as is the case for the copper data we have been discussing). So to make the most accurate measurements (smallest percent error), all systematic errors must be eliminated. Note that the percent error for a set of measurements can be made using the average. The average value of copper’s density, using the data that we have been discussing, is 9.55 g/cm3, which has +6.6% error.
The range is the simplest, and crudest, measure of the precision for a set or measurements. The range is simply the highest value minus the lowest value, and can be used to get a rough idea of the spread in the data, but not much more. Sometimes you will see a range reported in the form ± (range/2), which should not be confused with the confidence limits discussed below.
A better measurement of precision for a data set is the standard deviation (σ) which may be calculated using Eqn. 3 for data sets that have more than about 20 points.
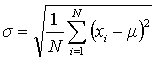 |
(3) |
In Eqn. 3 μ is the true mean (what the average becomes when N is large). Since it is rare in chemistry to have more than three to five replicate experiments, the estimated standard deviation, S, is used instead (Eqn. 4). In either case, a smaller S or σ indicates higher precision.
| |
(4) |
Note the dependence of both S and σ on the number of data points. If the difference terms are all about the same, then the precision should increase (S and σ decrease) as N increases. So, it is statistically advantageous to make more measurements, although this must be balanced with practical considerations. No one wants to do a ten-day experiment 30 times just to get better statistics!
The standard deviation is related to another estimate of precision known as the confidence limit or the confidence interval. The confidence interval is a range of values, based on the mean and the standard deviation of the data set, where there is a known probability of finding the “true” value. A confidence limit is written as ± Δ at the given confidence level. For example, a volume expressed as 2.16 ± 0.05 cm3 at the 95% confidence level means that there is at least a 95% probability of finding the “true” value in the range 2.11 cm3 to 2.21 cm3 (in other words, within ± 0.05 cm3 of the average, 2.16 cm3). It does not mean that only 95% percent of the time we are confident of the result! To some extent precision is separate from accuracy. However, if enough precise measurements are made in the absence of systematic error, we have increased confidence that our average is a good approximation to the true value, even though we do not know the true value. So, a confidence limit also expresses a level of certainty that the true value lies within ±Δ of the average, in the absence of systematic error.
To determine a confidence limit, the uncertainty, Δ, must first be calculated from the estimated standard deviation using Eqn. 5. The value of t in Eqn. 5 may be calculated in Excel using the TINV function, or may be taken from a table such as Table 1, which gives the value of t for various degrees of freedom (usually the number of data points minus one, i.e.,N – 1) at the 95% confidence level. Note that as the precision of a set of measurements increases, Δ will decrease at a set confidence level. Higher confidence levels also reflect higher precision in the data set.
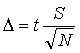 |
(5) |
| Degrees of Freedom | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 | ∞ |
| t | 12.7 | 4.30 | 3.18 | 2.78 | 2.57 | 2.45 | 2.36 | 2.31 | 2.26 | 2.23 | 2.13 | 1.96 |
Table 1. Values of t at the 95% confidence level for various degrees of freedom.
Precision and Significant Figures
In lecture and on exams and quizzes when we write a number, we assume that the precision is ±1 in the last number written (for example, the number 31.778 would be assumed to have a precision of ±0.001). We do this for simplicity. Because when we make this assumption we only need to concern ourselves with significant figures and we can ignore statistics and the propagation of error. In real life we are not so lucky and we must worry about significant figures, statistics and the propagation of error. However, significant figures are always our first step in analyzing our data.
The uncertainty in a number tells us directly how many significant figures our result has. This is because the uncertainty tells us in what place the first uncertain digit is (or you could say it is the first digit where certainty ends). For example, if you had a result 15.678±0.035 kJ/mole at the 95% confidence level, then you could tell from the uncertainty that the first digit that has any uncertainty in it is the tenths place. We know the 1, the 5 and the 6 (and are confident that we know them), but the 7 we have some doubt about. We only really know this digit to ±3 at 95% confidence and the hundredths place is not known with any certainty. How we show this is discussed below.
There are three ways in which the statistical information that accompanies a measurement (average, standard deviation, and confidence limit) can be stated. If, for example, five replicate measurements of a solid’s density were made, and the average was 1.015 g/cm3 with an estimated standard deviation of 0.006, then the results of this experiment could be reported in any of the following ways:
The average density is 1.015 g/cm3 with an estimated standard deviation of 0.006 g/cm3. The density is 1.015(6) g/cm3. The density is 1.015 ± 0.007 g/cm3 at the 95% confidence limit.
In this example the density has four significant figures, and the uncertainty is in the last decimal place. Sometimes the uncertainty and the number of significant figures in the measurement do not match. This means that each individual measurement was measured more exactly than the reproducibility within the group. If the standard deviation in the density experiment had instead been 0.010 g/cm3, then the results might be reported as:
The average density is 1.02 g/cm3 with an estimated standard deviation of 0.01. The density is 1.02(1) g/cm3. The density is 1.02 ± 0.01 g/cm3 at the 95% confidence limit.
The results have been rounded off because the number of significant figures does not reflect the precision of the data set. In other words, the statistical analysis shows us that the first digit where uncertainty begins is the 1/100ths place, even though each measurement was made to the 1/1000ths place. The last significant figure is in the 1/100ths place, so this is where rounding occurs. Sometimes the average and the uncertainties are quoted to the maximum number of significant figures (i. e., 1.015(10) g/cm3). In this way the precision of each individual measurement and the precision of the set of measurements are shown.
Using Statistics to Identify Hidden Gross Error
Another way in which statistics can be used is in the evaluation of suspect data by the Q-test. The Q-test is used to identify outlying (“bad”) data points in a data set for which there is no obvious gross error. The Q-test involves applying statistics to examine the overall scatter of the data. This is accomplished by comparing the gap between the suspect point (outlier) and its nearest neighbor with the range, as shown in Eqn. 6. The calculated Q is then compared to the critical Q values, Qc, at given confidence level, like those in Table 2. If the measured Q is greater than Qc, then that data point can be excluded on the basis of the Q-test.
| |
(6) |
| N | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Qc | 0.94 | 0.76 | 0.64 | 0.56 | 0.51 | 0.47 | 0.44 | 0.41 |
Table 2. Critical Q (Qc) values at the 90% confidence limit for a small number of data points, N.
For large data sets (N > 10) a data point that lies more than 2.6 times S (or σ) from the average may be excluded. Although for medium-sized data sets (between 11 and 15 data points), there is an alternative treatment that is usually sufficient. In these cases, we can use Qc for N = 10, but in doing so, a higher criterion is placed on the data for exclusion of a point than is required by statistics. So, an outlying point that could have been discarded is retained and the precision is quoted as being less than it actually is. But again, it is better to err on the side of caution in our data treatment.
In any case, only one data point per data set may be excluded on the basis of the Q-test. More than one point may be tested, but only one may be discarded. For example, you have measured the density of copper as 9.43, 8.95, 8.97, 8.96 and 8.93 g/cm3; can any of these points be excluded?
First, we must remember that the Q-test is only valid at the extremes, not in the middle of the data set. So before performing a Q-test, it is best to sort the data (as already been done with the data that we are considering). Now look at the extremes and see whether either of the points look odd. In this case, the low value (8.93 g/cm3) is not that much different than the values in the middle of the set, while the high value (9.43 g/cm3) looks to be suspect.
Having decided that the 9.43 g/cm3 value is suspect, we can calculate Q using Eqn. 6, (suspect value = 9.43, closest value = 8.97, highest value = 9.43 and lowest value = 8.93). This gives Q = 0.92 for this point. Since this exceeds Qcfor five data points (for N = 5, Qc = 0.64 in Table 2), this point may be excluded on the basis of the Q-test. The Q-test may not be repeated on the remaining data to exclude more points.
One last important thing about the Q-test is that it cannot be performed on identical data points. For example, if our data set had been 9.43, 9.43, 8.95, 8.97, 8.96 and 8.93 g/cm3, we would not have been able to use the Q-test on the 9.43 g/cm3 values.
So, now we have an average and an associated uncertainty at given confidence level for a data set. What happens if we use this result in a calculation? The simple answer is that the uncertainty carries through the calculation and affects the uncertainty of the final answer. This carrying over of uncertainty is called propagation of error, or propagation of uncertainty, and it represents the minimum uncertainty in the calculated value due entirely to the uncertainty in the original measurement(s). The equations that describe how the uncertainty is propagated depend on the calculation being done, and can be derived using calculus. Click here if you would like to learn more about how Eqn. 7 was derived. The following example demonstrates how a propagation of uncertainty analysis is done.
The dimensions of a regular rectangular wood block are 15.12 cm, 3.14 cm and 1.01 cm, all measured to the nearest 0.01 cm. What is the volume and the confidence limits on the volume based on this single measurement? The equation for the uncertainty in the volume is given in Eqn. 7, where ΔV, Δx, Δy and Δz are the uncertainties in the volume and the x, y and z dimensions, respectively. Do not be confused by the notation! The Δ represents the uncertainty, not a change, in these parameters. Since each measurement was made to the nearest 0.01 cm, Δx = Δy = Δz = ±0.01 cm. First we calculate the volume, being careful with our significant figures (note the extra “insignificant” figures from the calculator output, shown as subscripts, carried along in the calculation for rounding purposes).
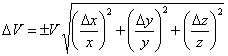 |
(7) |
Substituting the known values of V, x, y, z, Δx, Δy and Δz into Eqn. 7 gives
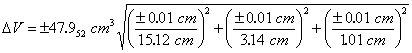 |
| |
| |
| |
So, the volume would be reported as 48.0 ± 0.5 cm3 for the single measurement, and this represents a minimum uncertainty in the volume based on the uncertainties in the block’s dimensions. Note that the propagated uncertainty usually has only one significant figure.
To see how the propagated uncertainty differs from an uncertainty for a population (data set), imagine that we did this measurement three times and got volumes of 48.1, 47.8 and 48.3 cm3. Each individual measurement has an uncertainty of ±0.5 cm3, from the propagation of uncertainty analysis, but the uncertainty for the set of measurements is±0.7 cm3. This was calculated with S = 0.3 cm3 (determined using Eqn. 4) and the value of t taken from Table 1 (for N – 1 = 2) by substitution into Eqn. 5. Thus, the volume would be reported as 48.1 ± 0.7 cm3 at the 95% confidence limit. Notice that the uncertainty in the population is not the same as the uncertainty in each individual measurement. They are not required to be the same, nor are they often the same. In this example, the propagated uncertainty is less than that for a series of volume measurements, indicating another source of uncertainty besides that arising from the uncertainty in the block’s dimensions. This is often the case, and in your conclusions to an exercise or experiment you should try to identify its source and discuss its impact on your result.
Regression Analysis
Once we have data from an experiment, the challenge is to determine the mathematical expression that relates one measured quantity to another. The problems that confront us when we attempt to mathematically describe our data are 1) how to establish the mathematical formula that connects the measured quantities and 2) how to determine the other parameters in the equation. The process by which a mathematical formula is extracted from a data set is called fitting, or regressing, the data.
A linear relationship is the simplest, and most useful, mathematical formula relating two measured quantities, x (the independent variable) and y (the dependent variable). This means that the equation takes the form y = m•x + b, wherem is the slope of the line and b is the intercept. It is possible to relate two quantities with other equations, but unless there is a good theoretical basis for using another function, a line is always your best initial choice. For a linear relationship the values of m and b must be found from the data (x and y values), which is done through a linear least squares regression (or fit). The mathematics behind the fitting algorithm is not relevant at this time, but it is important to know that the least-squares procedure assumes that the uncertainty in the x values is less than the uncertainty in the yvalues. This means that, if we want to get a meaningful slope and intercept from our fit, we must make the measured quantity with the smallest uncertainty be the independent variable.
Some of pitfalls that you may encounter when performing a regression analysis (and why it is always a good idea to graph your data) have been discussed by Anscombe.7
References
1. Click here to obtain this file in PDF format (link not yet active).
2. Paul, R. L.; Elder, L. A Miniature Guide for Students and Faculty to Scientific Thinking; Foundation for Scientific Thinking: Dillon Beach, CA, 2003.
3. Devore, J.; Peck, R. Statistics: the Exploration and Analysis of Data; Duxbury Press: Belmont, CA, 1993.
4. Skoog, D. A.; West, D. M.; Holler, F. J.; Crouch, S. R. Analytical Chemistry: an Introduction; Harcourt College Publishers: New York, 2000.
5. Harris, D. C. Quantitative Chemical Analysis; W. H. Freeman: New York, 2003.
6. Andraos, J. J. Chem. Educ. 1996, 73, 150-154. Click here to view this article on the Journal of Chemical Education web page (Truman addresses only).
7. Anscombe, F. J. The American Statistician 1973, 27, 17-21. Click here to view this article on JSTOR. The Wikipedia entry for Anscombe’s quartet summarizes the results nicely.
Last Update: November 5, 2013
