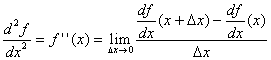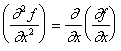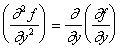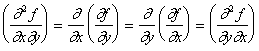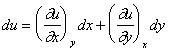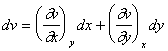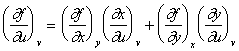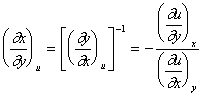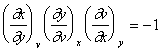Calculus Review for Physical Chemistry

Partial Derivatives and Differentials for Physical Chemistry

Adapted from material prepared by the physical chemists at the University of Kansas by J. M. McCormick

Last Update: July 3, 2006

In physical chemistry it is generally necessary to view certain quantities (such as energy, enthalpy and entropy) as functions of several variables. For example, if the energy of a single component system is thought of as a function of the number of particles, N, the volume, V and the entropy, S; thus we may write E = ƒ(N, V, S). The manipulation of such functions requires multivariate calculus. The purpose of this paper is to review single variable calculus, and its extensions to multiple variables. The information provided below, along with that found in your text, should be sufficient for you to fully understand the material that will be presented in physical chemistry.

Derivatives and Differentials for One Variable

We have a function ƒ of one variable x denoted ƒ(x). The derivative of ƒ at point x is:

(1)

The derivative, denoted , is also a function of x.

From the definition of the derivative we can see that for small variations of x, the corresponding variations of ƒ will be:

(2)

The above equation becomes exact in the limit of Dx → 0, that is when Dx becomes infinitesimally small. In that limit, Dƒ is also infinitesimally small, but still proportional to Dx. We denote this limiting behavior by writing the change in x as dx. The corresponding change in ƒ will also be infinitesimal; we denote it by dƒ and call it the differential of ƒ:

(3)

Thus, writing down the differential of ƒ allows us to calculate changes in the value of ƒ corresponding to small variations of the variable x.

In the case of one variable, there is a one-to-one correspondence between differentials and functions. This means, that given a differentiable function ƒ, we can calculate dƒ according to Eqn. 3. And vice-versa, if we have an expression for the variation of a quantity g in the form:

(4)

where M(x) is a function of x, then g is a function of x and M(x) = dg/dx.

Example 1:

Define the function f(x) as follows: or

Now let x = 2.00 and dx = 0.01. The exact result is then:

Dƒ = ƒ(2.01) – ƒ(2.00) = 4.04 -4.00 = 0.04

while using the differential gives:

dƒ(x = 2.00) = 2 x dx = (2)(2.00)(0.01) = 0.04

The second derivative is a simple extension – it is the derivative of the derivative:

(5)

Derivatives and Differentials for Two Variables

Partial Derivatives

Let ƒ now be a function of two variables x and y: ƒ(x,y). We can define two types of first derivatives for x, which we call partial derivatives of ƒ with respect to x and with respect to y:

(6)

(7)

The way to think about partial derivatives is to consider variation of ƒ upon changes in one variable only, while the other(s) are treated as constants.

Second partial derivatives can also be defined, this time there are three types:

(8)

(9)

(10)

where the last equation indicates that the mixed derivatives and are equal (i. e., the result of taking derivatives is independent of the order of the operations).

Example 2:

Here we check that the two ways of calculating the mixed derivative will actually give the same result. We can also see explicitly that the partial derivatives are functions of x and y.

Let f be a function of x and y defined as follows .

The first derivative of this function with respect to x is while the first derivative with respect to y is .

The second derivatives with respect to x and y are, respectively, and .

The mixed derivatives are .

The Differential

We want to know what will be the change in ƒ upon small variations of x and y, and arrive at the following equation:

(11)

Again, this equation becomes exact for infinitesimally small Dx and Dy, with corresponding change in ƒ called the differential dƒ:

(12)

Example 3:

Let f be a function of x and y defined as follows

Calculate the change in ƒ when (x, y) change from (2, 2) to (2.1, 2.1).

Exact result:

Using the differential:

Exact Differentials

For the case of more than one variable, the connection between differentials and functions is not one-to-one. For a given differentiable function ƒ(x,y), we can write down the differential using partial derivatives, as defined above. However, just because we might come up with an expression for the variation of a quantity g of the type given in Eqn. 13 does not mean that g is a function of x and y! (Alternatively, there might not exist a function having this differential).

(13)

For dg to be a differential of a function, also called an exact differential, the following condition must hold:

(14)

If the above condition (called the Euler condition) holds, then dg is an exact differential, and

(15)

(16)

The Euler condition is a simple consequence of the symmetry of the mixed derivative of a function with respect to x and y.

Example 4.

A fixed amount of gas in a cylinder may be described by two variables, the volume, V, and the pressure, P. We have derived an expression for an infinitesimal amount of work done on the system in a reversible process as dW = – PdV. Is this expression an exact differential?

Since we have two variables V and P, the full expression for dW is really:

(17)

We have now obtained an expression for small changes in W corresponding to small changes in V and P of the form given by Eqn. 13 with M(V, P) = -P and N(V, P) = 0.

We can now check if Euler’s condition holds:

(18)

(19)

The conclusion is that the mixed derivatives are not equal, dW = -P dV is not an exact differential. To denote this we sometimes write dW instead of dW.

An alternate statement is that there is no function W(P, V) which can have a differential of this form, which is equivalent to saying work is not a state function. The same holds true for heat transfer (consider dQ = C(P, T) dT).

Properties of Partial Derivatives

The Chain Rule

We have a function ƒ of two variables x and y: ƒ(x, y). The differential dƒ is then:

(20)

Now suppose we want to express the derivatives and differential using different variables u and v, where u = u(x, y) and v = v(x,y):

(21)

We can express dx and dy in terms of du and dv from the relationships x = x(u, v) and y = y(u, v) analogously to Eqn. 2:

(22)

(23)

Upon substitution into Eqn. 1 and comparison with Eqn. 2

(24)

This is known as the chain rule and is the basic equation for changes of variables in partial derivatives. An analogous formula can be obtained for by exchanging u with v in Eqn. 24.