Liquid-Vapor Equilibrium of a Binary System
Adapted by J. M. McCormick from an exercise used at the University of Kansas.
Last Update: December 19, 2012
Introduction
The understanding of the equilibrium between the liquid and vapor phases in a multi-component system is important industries ranging from brewing to petroleum refining. In this exercise you will be examining the chloroform-acetone system and comparing your results to literature values. You are referred to the literature for more information on the theory involved.1-3
Procedure
The procedure is similar to that described in the literaure.1,2 However, instead of the apparatus described in these references, the one shown in Fig. 1 will be used. The modified apparatus is designed so that there is very little liquid hold-up and that the small amount of liquid that is condensed from the vapor has almost the same composition as the vapor. The apparatuses described in the literature either require that a substantial amount of liquid be vaporized and condensed (which causes the liquid and vapor compositions to change continuously and so the condensate composition is a rather poor representation of the vapor composition and the temperature changes continuously, which introduces an unacceptably large uncertainty into the results),1 or are too expensive to construct.2
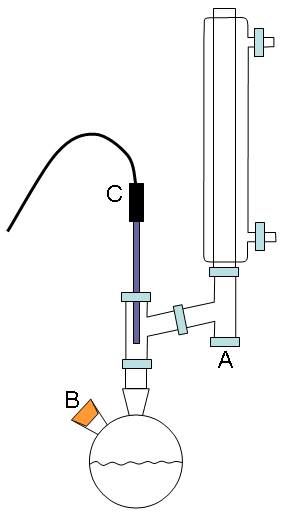 |
 |
Figure 1. Distillation apparatus to be used in this exercise (schematically on the left and an actual view on the right). The hoses that supply water to the condenser have been removed and the optional aluminum foil wrapping are not shown in the photograph of the apparatus for the clarity’s sake.
In the kit for this exercise you will find the items listed in Table 1. Please check that everything is present and in good condition before beginning.
| Number | Item |
|---|---|
| 1 | 100 ml 19/22 Two-neck round bottom flask |
| 1 | 10 ml Glass syringe |
| 1 | 1 ml Hamilton gas-tight syringe |
| 1 | Short needle in a protective case |
| 1 | Long needle |
| 1 | Blue (19/22) Keck clip |
| 1 | Distillation assembly (includes o-ring) |
| 1 | Vial containing 13 mm septum liners |
| Several | Septum stoppers |
| 1 | Vernier temperature probe |
| 1 | Vial of boiling chips |
| Several | Small vials |
Table 1. Equipment needed for this exercise included in the kit.
Calibrate the temperature probe at three points (0 °C, room temperature, and 100 °C are convenient). Helpful hint: the calibration of the temperature probe can be done while the apparatus is being assembled. Click here to review operation of the LabPro and the LoggerPro software that controls it.
Assemble the distillation apparatus as shown in Fig. 1 (check with the instructor for assistance). You may wish to wrap the glass portions of the reflux apparatus below the condenser with aluminum foil to help obtain a stable reflux temperature. Place a septum liner on the vapor condensate collection arm (A in Fig. 1) and a septum stopper in smaller arm of the round bottom flask (B in Fig. 1). Insert the temperature probe through the orange retaining nut and then through an o-ring. Carefully place it in position (C in Fig. 1) such that the temperature probe is upright (a small clamp will be needed) and the o-ring is not kinked or bent, and then gently tighten down the retaining nut. In addition to the small clamp on the temperature probe, you should clamp the apparatus just above the neck of the round bottom flask and on the condenser, as shown in Fig. 1. The blue Keck clip should be used to hold the round bottom flask to the distillation head.
Load the flask with 40 ml CHCl3 (for the CHCl3-rich solution), or 30 ml acetone (for the acetone-rich solution) and a few boiling chips. CAUTION! Both CHCl3 and acetone are highly flammable, and CHCl3 has adverse health effects. Carefully start heating the flask until reflux begins. Record the barometric pressure now, and at several additional times during the course of the experiment (ideally this should be done before a sample is taken). Apply the correction to the pressure indicated on the barometer.4
When liquid is seen refluxing in the lower portion of the condenser and the temperature reading is stable (i. e., remains unchanged for several minutes), record the temperature. Confirm that the temperature corresponds to the boiling point of the liquid in the distillation apparatus. Using a clean, dry syringe equipped with the long needle, remove a sample (approximately 0.05 mL each) from the liquid that has collected below the condenser (representing the vapor’s composition) and from the distillation flask (liquid composition). It is advised that you first remove the condensate (through the top of the condenser using the long pipetting needle), and then remove the sample from the distillation flask. Do not leave the needle poking through the septum afterwards. Carefully place the samples in marked vials and immediately measure the index of refraction of each sample using the Abbé refractometer. Evaporation of the sample in the refractometer can be a problem, so work quickly. Confirm that the condensate and the liquid in the distillation flask have the same index of refraction and that both match the literature value for the solvent in the flask. This procedure serves two purposes: 1) it allows us to find any systematic error (and determine any correction factor to apply), and 2) the instrument will then be set near to the index of refraction to be measured, thus minimizing the time needed to make each subsequent measurement.
The index of refraction as a function of the mass percent of chloroform in acetone-chloroform mixtures is given in Table 2 (click here to download this table as an Excel file). If your index of refraction lies between two tabulated values, you may make a simple linear extrapolation from the two nearest tabulated points. An alternative method is to fit the index of refraction data to an empirical function in mass percent chloroform in Excel or LoggerPro, and then simply use this function to find the composition from a measured index of refraction.
| np20 | %CHCl3 | np20 | %CHCl3 | np20 | %CHCl3 | np20 | %CHCl3 |
|---|---|---|---|---|---|---|---|
| 1.3562 | 0.00 | 1.3780 | 23.50 | 1.4000 | 47.55 | 1.4220 | 72.85 |
| 1.3570 | 0.75 | 1.3790 | 24.60 | 1.4010 | 48.70 | 1.4230 | 74.10 |
| 1.3580 | 1.75 | 1.3800 | 25.65 | 1.4020 | 49.80 | 1.4240 | 75.30 |
| 1.3590 | 2.75 | 1.3810 | 26.70 | 1.4030 | 50.90 | 1.4250 | 76.50 |
| 1.3600 | 3.80 | 1.3820 | 27.80 | 1.4040 | 52.00 | 1.4260 | 77.70 |
| 1.3610 | 4.85 | 1.3830 | 28.85 | 1.4050 | 53.10 | 1.4270 | 78.95 |
| 1.3620 | 5.90 | 1.3840 | 29.95 | 1.4060 | 54.20 | 1.4280 | 80.20 |
| 1.3630 | 7.00 | 1.3850 | 31.00 | 1.4070 | 55.30 | 1.4290 | 81.40 |
| 1.3640 | 8.10 | 1.3860 | 32.05 | 1.4080 | 56.45 | 1.4300 | 82.65 |
| 1.3650 | 9.20 | 1.3870 | 33.15 | 1.4090 | 57.60 | 1.4310 | 83.90 |
| 1.3660 | 10.30 | 1.3880 | 34.25 | 1.4100 | 58.75 | 1.4320 | 85.15 |
| 1.3670 | 11.40 | 1.3890 | 35.30 | 1.4110 | 59.90 | 1.4330 | 86.40 |
| 1.3680 | 12.50 | 1.3900 | 36.40 | 1.4120 | 61.05 | 1.4340 | 87.70 |
| 1.3690 | 13.60 | 1.3910 | 37.50 | 1.4130 | 62.25 | 1.4350 | 89.00 |
| 1.3700 | 14.70 | 1.3920 | 38.60 | 1.4140 | 63.40 | 1.4360 | 90.35 |
| 1.3710 | 15.80 | 1.3930 | 39.75 | 1.4150 | 64.55 | 1.4370 | 91.65 |
| 1.3720 | 16.90 | 1.3940 | 40.85 | 1.4160 | 65.75 | 1.4380 | 93.00 |
| 1.3730 | 18.00 | 1.3950 | 42.00 | 1.4170 | 66.90 | 1.4390 | 94.35 |
| 1.3740 | 19.10 | 1.3960 | 43.10 | 1.4180 | 68.10 | 1.4400 | 95.75 |
| 1.3750 | 20.20 | 1.3970 | 44.25 | 1.4190 | 69.30 | 1.4410 | 97.20 |
| 1.3760 | 21.30 | 1.3980 | 45.35 | 1.4200 | 70.50 | 1.4420 | 98.55 |
| 1.3770 | 22.40 | 1.3990 | 46.45 | 1.4210 | 71.70 | 1.4431 | 100.00 |
Table 2. Refractive index of acetone-chloroform mixtures as a function of the mass percent chloroform in the mixture.
Add 5 ml of acetone or CHCl3, whichever is appropriate, to the flask through the septum stopper at B via syringe. After the system has stabilized, remove a sample of the distillate and a sample from the flask and measure the index of refraction of each. Repeat the addition, equilibration and withdrawal of sample steps at least five or six times. By working efficiently you should be able to complete the CHCl3-rich portion in the first week, the acetone-rich portion in the second week and in the third week obtain additional data to correct any gross errors from the first two weeks or to improve data quality. As you are attempting to measure accurately and precisely the composition and boiling point of the azeotrope, it is advisable to overlap the regions studied and to use the third week to improve the quality of your data. To overlap the data, one could keep adding CHCl3 to the acetone when you are doing the acetone-rich system to make the solutions CHCl3-rich. It is easier to sequentially add one component to the flask to give a new mixture than it is to make up a fresh mixture each time. However, it is critical that only the minimum amount (~0.05 ml) of the distillate and the solution in the flask be removed for analysis. If the total volume is sufficiently large and amount withdrawn is small, you do not need to correct for the material removed, but this assumption should be checked during the experiment.
When work for the day has been completed, allow the flask and the reflux apparatus to cool to room temperature, disassemble the set up and return it to the storage box. Place all liquids in the appropriate waste solvent container. Remove and discard the septum. Examine the septum liner, and discard it if damaged.
Results and Analysis
Prepare a liquid-vapor phase diagram (temperature as a function of the liquid’s composition). It is highly recommended that you prepare this diagram as you obtain the data. In this way you can correct any gross errors immediately. The data points should form four smooth curves (one for the liquid and one for the vapor on either side of the azeotrope) with minimal deviations from the curve. Note that none of these lines are expected to be straight.1 The final version of your diagram, showing your fits to the data, must be included in the Results section of your report. You also must report the azeotrope’s composition and boiling point and their accepted values.5
While you can model the relationship between the temperature and composition for each phase using four separate empirical equations to predict the azeotrope’s composition and boiling point, the data may be modeled based on the physical properties of the liquids.2 We can write the total pressure for a non-ideal system consisting of two liquids, A and B, using Dalton’s law of partial pressures as Eqn. 1, where Ptot is the total pressure, PA0 and PB0 are the vapor pressures of the pure liquids, γA and γB are the activity coefficients of each compound in the liquid mixture, and χA andχB are the mole fractions of the compounds in the liquid phase (note that the mole fraction of component i in the vapor phase would be yi = Pi/Ptot).
| |
(1) |
The two-parameter van Laar equation for a binary system can be used to model the activity coefficients, and these are shown for each component as Eqn. 2, where the parameters kAB and kBA take into account molecular size and the interactions between the molecules.6
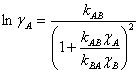 |
(2a) |
 |
(2b) |
It is possible to determine the values of kAB and kBA, if we know the composition of the azeotrope, because the activity coefficient of each component at the azeotropic composition, γA,az and γB,az, is related to its vapor pressure at the azeotrope’s boiling point (P0A,az and P0B,az) and the total pressure at the azeotrope’s boiling point, Paz, by Eqn. 3.
| |
(3a) |
| |
(3b) |
Making this substitution and rearranging gives Eqn. 4, where χA,az and χB,az are the mole fraction of each component of the liquid mixture with azeotropic composition. We could simplify the equations further, if we wish, by remembering that since this is a binary mixture χA + χB = 1 (and thus χA,az + χB,az = 1).
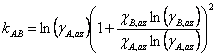 |
(4a) |
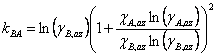 |
(4b) |
If you now refer back to Eqn. 1, you will see that we have relationships between most of the variables in this expression. The only things that are missing are the vapor pressure of each liquid at each temperature. However, we can calculate these using the Antoine equation (Eqn. 5) using information available on-line at NIST. In Eqn. 4, a, b andc are empirical parameters that are unique to a compound, T is the temperature (either in Celsius or Kelvin) and P is the vapor pressure (usually in bar).
| |
(5) |
You have data that consists of temperature and the composition of the liquid at some ambient pressure. Since boiling is occurring, we know that Ptot and the ambient pressure must be the same. If you substitute Eqn.s 4 and 5 into Eqn. 1, you will then have an equation that relates the pressure at which boiling occurs (which you measured) with the composition of the liquid (which you measured), the azeotropic composition and the temperature. Since this equation could be written for each of your data points, you will have a system of equations that could be iteratively solved for the composition of the azeotrope and its boiling point. This may be done in Excel, or other mathematical software package, although a spreadsheet may be the easiest way to enter the data and perform the calculations. If you use Excel’s Solver package, you will need to provide a starting point for the fitting routine, which you can obtain by estimating χA,az,χB,az and T from your data. See reference 2 for more information and helpful hints on how to perform this fit.
References
1. Garland, C. W.; Nibler, J. W. and Shoemaker, D. P. Experiments in Physical Chemistry, 7th Ed.; McGraw-Hill: New York, 2003, p. 208-215.
2. Halpern, A. M. and McBane, G. C. Experimental Physical Chemistry, 3rd Ed.; W. H. Freeman: New York, 2006, p. 14.1-14.14.
3. Atkins, P. and de Paula, J. Physical Chemistry, 8th Ed.; W. H. Freeman: New York, 2006, p. 179-184.
4. Brombucher, W. G.; Johnson, D. P. and Cross, J. L. Mercury Barometers and Manometers, National Bureau of Standards Monograph 8; Washington, D. C., 1960.
5. CRC Handbook of Chemistry and Physics, 64th Ed.; Chemical Rubber Company: Boca Raton, FL, 1983, p. D13.
6. Prausnitz, J. M.; Lichtenhaler, R. N. and de Azevedo, E. G. Molecular Thermodynamics of Fluid-Phase Equilibria, 3rd Ed.; Prentice Hall: Upper Saddle River, NJ, 1999, p. 250-254.
