Kinetics of Crystal Violet Bleaching1, 2
Authors: V. C. Dew and J. M. McCormick*
Last Update: March 12, 2013
Introduction
Chemists are always interested in whether a chemical reaction can occur and exactly how it occurs. The first question is answered though thermodynamics, as you saw in a previous laboratory exercise, while the second is the domain of kinetics. In a kinetics experiment, a chemist attempts to understand the step-by-step transformation of reactants to products. Taken together these elementary steps gives us the mechanismby which the reaction proceeds. Note that a reaction’s kinetics are very much tied to the pathway the reactants take to the products (i. e., the mechanism), which is very different from the reaction’s thermodynamic properties (i. e., ΔH, ΔS and ΔG) that do not depend on the path. While the thermodynamics and kinetics of a reaction may at times seem complementary, and at other times seem contradictory, it is always important to have a detailed understanding of both.
In this experiment you will determine the rate law for a chemical reaction. The rate law is a mathematical expression that relates the amount of time it takes a reaction to happen to the concentrations of the starting materials. The disappearance of reactant over time depends on the rate constant, and the concentration of each reactant raised to some power. This power is known as the order with respect to that reactant. The sum of the individual orders is the overall order of the reaction. The order of reaction with respect to each reactant, as well as the rate law itself, cannot be determined from the balanced chemical equation; each must be found experimentally (More Info). The rate law is the basic equation of kinetics and it will be the standard against which we judge possible mechanisms.
Scheme 1. Reaction of crystal violet with OH–.
In this experiment you will determine the rate law for the reaction of the dye crystal violet (CV) with OH– in aqueous solution according to the balanced net ionic equation given in Scheme 1. We will define the rate of reaction as the disappearance of the colored CV over time, which can be expressed in differential form as d[CV]/dt. So, the rate law for this reaction can be written as shown in Eqn. 1 in terms of the concentrations of CV and OH– and the rate constant for the reaction, k. In writing this equation we assume that both CV and OH– are involved in the reaction (that is x and y are both not zero and are likely integers), but only the experiment will tell us whether these assumptions are valid.
 |
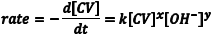(1) |
The point of any kinetics experiment is to determine the order with respect to each reactant (i. e., find x and y) and to find the value of k. This is a problem if we have more than one reactant (as we do here), in which case the isolation method is often used. The isolation method entails making the concentration of all but one of the reactants very high (so their concentrations do not change appreciably over the course of the reaction). The order with respect to the isolated reactant is then determined. The process is then repeated, isolating each of the other reactants in turn, until all of the orders have been determined.
In this experiment we will make the [OH–] very large and, therefore, essentially constant. We can then simplify Eqn. 1 to Eqn. 2, where we have defined a new rate constant, kobs, which is the observed rate constant at some specific [OH–]. The relationship between kobsand the intrinsic rate constant, k, for this reaction is given by Eqn. 3.
 |
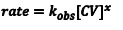(2) |
 |
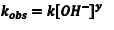(3) |
Under conditions of high, constant [OH–], the order with respect to CV can be determined by graphically applying the integrated rate laws (More Info). Since the absorbance of a CV solution is directly proportional to the concentration of CV, according to Beers’ Law, (More Info) the actual [CV] can be replaced by Amax, the solution’s maximum absorbance (somewhere around 600 nm). A graph of Amax as a function of time will give a straight line if the reaction is zero-order in CV (x = 0). If the reaction is first-order in CV (x = 1), then a graph of ln(Amax) as a function of time is linear. And finally, if a graph of 1/Amax as a function of time is linear, it indicates that the reaction is second-order with respect to CV (x = 2). In each case, if a particular relationship is linear, then the slope of that graph can be used to determine kobs. Note that only one of these three graphs will be linear!
In some instances it is not possible to isolate one of the reactants, because the concentration of that reactant must remain high for the system to behave predictably, as is the case here. However, the order of the reaction with respect to OH–, and k, can still be found. First we need to change Eqn. 3 into an easily-graphed form by taking the logarithm of both sides to give Eqn. 4 (note that the natural logarithm would also work). To determine the order with respect to OH– and k, we first perform the kinetics experiment at different, albeit still high, OH– concentrations and then graph log(kobs) for these reactions as a function of log[OH–]. The slope of this graph is y, the order with respect to OH–, and the intercept is log(k).
 |
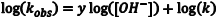(4) |
In this experiment each you will work in a group with the other students at your laboratory table. Each group will measure the absorbance of CV as a function of time at a different assigned hydroxide concentration using an Ocean Optics spectrometer. Each group will determine the order of reaction for CV at their [OH–]. The class data (kobs at different [OH–]) will then be pooled and used to determine the order with respect to OH- and the intrinsic rate constant.
Experimental 2 
Upon arrival in class you will be assigned hydroxide concentrations (either 0.050 M, 0.040 M, 0.030 M, 0.025 M, 0.010 M or 0.0050 M). Before you come to the laboratory, work out the dilution you will need to do to prepare 50.0 mL of each of these solutions by dilution of a 0.050 M NaOH stock solution. Also review the Ocean Optics spectrometer’s operating instructions before coming to class.
Prepare your assigned concentration in a beaker using graduated cylinders for measuring the stock solution and the required volume of water. CAUTION! The NaOH solution is caustic. Stir the solution and cover the beaker with a watch glass.
Obtain approximately 40 mL of the stock CV solution in a clean and dry beaker.CAUTION! Crystal violet will stain skin and clothing! Record the concentration of CV (it should be around 2 x 10-5 M).
Prepare the spectrometer and computer to collect absorbance data as described on the Ocean Optics page (the instrument should be already connected to a computer and warming up when you arrive). Use distilled water as the reference in the same cuvette that you will use for the rest of your measurements. Dilute 10 mL of the CV solution with 10 mL of distilled water in a small beaker and mix well. Rinse a cuvette three times with small portions of this solution and then fill the cuvette approximately three-quarters full. Remove any bubbles by gently tapping the cuvette with your finger. Under absolutely no circumstances are you to tap a cuvette on a table top. Before placing the cuvette in the spectrometer, be sure to thoroughly wipe the cuvette’s clear sides with a Kim-Wipe (do not use a paper towel). Obtain the solution’s absorption spectrum. Use the cursor to determine the point of maximum absorbance, which should be near 600 nm. Record this value in your notebook. Save the absorption spectrum to print later (from Excel) and include in your notebook.
Now set up the spectrometer to record the change in absorption at the wavelength of maximum absorption. The instrument does not need to be set for a delay or for triggering, but do select the option Sample at Time Zero in the main Data Collectionsetup window once you have selected a time-based measurement.
Transfer 10 mL of your NaOH solution to a clean, dry beaker. Add 10 mL of the crystal violet solution and stir the resulting reaction mixture well. Rinse a cuvette three times with small portions of the reaction mixture and fill the cuvette three-quarters full with the reaction mixture. Wipe the outside of the cuvette with a KimWipe and place the cuvette in the spectrometer’s cell holder. Push the Collect button 
to start the kinetics run. You will need to work efficiently so as to not lose too much data while you are preparing the cuvette. The spectrometer will record the absorbance as a function of time and save the data to the file you specified. CAUTION! Do not adjust any of the spectrometer settings during a kinetics run; it will ruin your data.
When the kinetics run is over, discard the reaction mixture as instructed and then clean and dry the beaker in which you ran the reaction. Select your data in LoggerPro’s data window and copy and paste them into an Excel worksheet. Prepare a graph of absorbance as a function of time and show it to your instructor. When your results have been approved, obtain two more kinetics data sets with your assigned [OH–] (for a total of three). While you are performing these runs, you can be working up the previous data as described below. Note that one or two groups may need to change the length of their kinetics run, if practical, depending on their [OH–]. What groups are they and why must they change the length of their runs?
IMPORTANT! Do not throw away your hydroxide or CV solutions until you have prepared all three graphs for all three runs. Once you are convinced that your result are valid, you may discard these solutions as directed by your instructor.
Results and Analysis
Prepare three graphs for the first run: the first graph is Amax as a function of time, the second is ln(Amax) as a function of time, and the third is 1/Amax as a function of time. One of these graphs will give a straight line; from this graph determine order with respect to crystal violet at your [OH–] and the rate constant, kobs. Compare your results to other groups in the laboratory. Do you get results that are consistent (that is do all groups have the same graph being linear, does the rate of reaction go up with increasing [OH–], etc.)?
Prepare graphs for the other two runs, but you only need to prepare the graph that gave you a linear result for the first run (i. e., if the second-order integrated rate law graph was linear for the first run, then you only need to do a second-order integrated rate law graph for each of the other two runs). Average your three kobs, determine the estimated standard deviation and the uncertainty at the 95% confidence level. Share your results with the rest of the class and then prepare Table 1 in your notebook using the class data.
| [OH-1] (M) | kobs | |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Table 1. Model table to summarize the class data; your table may have up six rows of data. Note that kobs‘s units have been omitted; determine them and place them in your table (like shown for the column containing the [OH–]).
From the class data at different [OH–], prepare a graph of log(kobs) as a function of log[OH–] to determine the order of reaction with respect to OH–. You do not need to determine the uncertainty in k.
Print out the absorbance spectrum of CV using Excel with absorbance (no units necessary) as a function of wavelength (units are nm). Set the x-axis so that only the absorbance in the range 450 to 900 nm is displayed. Set the y-axis so that the absorbance near 600 nm is clearly seen (choose the scale so that Amax is about three-quarters of the full y-axis).
Conclusions
The conclusion should use the outline for a measurement exercise.
Use Tables 2 as a model for your Summary Table.
| Order with respect to CV | Order with respect to OH- | k | |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 |
Table 2. Model Summary Table for this exercise. Note that you will need to determine the units on k and put them in the column heading.
References
1. Click here to obtain this experiment in PDF format. Note that hyperlinks are not active in the pdf version. 2. Holmquist, D. D. and Volz, D. L. Chemistry with Computers: Using Logger ProTM; Vernier Software: Portland, OR, 1997, p. 30-1 ff.