Binary Solid-Liquid Phase Diagram
Author: J. M. McCormick
Last Update: August 11, 2009
Introduction
Solid-liquid phase diagrams show the phase relationships in mixtures of two or more components and are very important in understanding the behavior of mixtures in metallurgy, material science and geology. In this exercise, you will measure cooling curves of either the napthalene-biphenyl system (group 1) or the napthalene-durene (1, 2, 4, 5-tetramethylbenzene) system (group 2). From these data you will generate the phase diagram for the system and determine ΔfusH and the melting point for the two pure substances in your system.
Procedure
CAUTION! Pay careful attention to the health and safety cautions accompanying the substances used in this exercise. Take care when handling these compounds to minimize everyone’s exposure to these substances.
The kit for this exercise that contains supplies (1 Vernier temperature probe and 2 small test tubes) for two groups to work on this exercise separately. If two groups will be working simultaneously on this exercise, please coordinate your activities with the other group.
You will be recording the temperature as a function of time using a Vernier temperature probe interfaced to a computer running the LoggerPro software package through the LabPro interface. Click here to review the use of the temperature probe and the LoggerPro software. Each day you will need to perform a three-point (0 °C, room temperature, and 100 °C are convenient) calibration of the the temperature probe to assure accurate and precise readings. Choose the LoggerPro acquisition parameters so that you take enough data to clearly see the break and arrests in the cooling curve.
Precisely weigh out the appropriate amount of each substance to achieve the desired mole fraction (maximum mass should be less than about 3 g). Place the substances in the sample holder (a small test tube) and heat to melting (a beaker of hot/boiling water is sufficient for this). Mix well. Place the temperature probe in the sample and start recording the temperature. The key to high quality results in this exercise is slow cooling to prevent supercooling1,2 and to allow for observation of the breaks and arrests. The rate may be about 1 °C/min, but it may be more, or less, depending on the system. The literature1,2,3 suggests using an ice bath to speed the cooling process; you can decide whether this is a wise choice. The sample must also be stirred as it cools, which is best accomplished manually. The temperature probe works well as a stirring rod as does a piece of wire bent into a loop at the end. It is highly recommended that you visually monitor the sample throughout the cooling process as the breaks may be difficult to recognize from the cooling curves alone, but the formation of a solid from the melt is visually very obvious.
Prepare enough samples to cover the range of mole fractions required to prepare the phase diagram. It is suggested that you start with one of the pure substances in the first week, measure its cooling curve, and then add more of the other component to form a new mixture. Treat the new sample as described above. This method will cut down on the amount of material used in your analysis, but extreme care must be taken because if any sample is lost during the previous run the new mole fraction (and thus your data from there on) will be erroneous. If you lose any sample during a run, you will need to prepare a fresh sample at the next composition. In the second week of the exercise repeat the process with the other component. You are advised to have the two data sets overlap (have several compositions in both data sets be the same) and to check the data for consistency after each week’s work so that you may correct any errors.
Depending on how ideally your mixture behaves, you may need to obtain several points at low and high mole fractions of one component of the mixture to facilitate the determination of ΔfusH for each component. It is, therefore, beneficial to graph your data as you obtain it, and once you have obtained enough data, try fitting it, as described below.
Dispose of the waste in the appropriate bottle. It may be necessary to use a solvent (such as acetone) to thoroughly clean the sample container, and this must also be disposed of properly. Under NO circumstances are the organic solids to be placed in a trash can or flushed down the drain.
Results and Analysis
Figure 1. Generalized solid-liquid phase diagram for a binary system comprised of compound A and compound B. The isopleths labeled 1, 2 and 3 correspond to the cooling curves shown in Fig. 2.
If we consider a binary solid-liquid system composed of compound A and compound B in which the solids are essentially insoluble in each other (this means that the solid state is composed of the two solids existing in their own separate, pure states), we may draw the phase diagram shown in Fig. 1 at some constant pressure. Cooling curves along the isopleths labeled 1, 2 and 3 are shown in Fig. 2. Note the existence of both short irregularities in cooling curves 1 and 3 in Fig. 2, known as breaks, and regions where the temperature is constant for longer periods of time, known as arrests or halts. The breaks in the cooling curves along isopleths 1 and 3 correspond to temperatures where a pure solid is beginning to crystallize out of the liquid melt. In the case of cooling curve along isopleth 1, it is pure compound A that is crystallizing, while in the cooling curve along isopleth 3, it is pure compound B crystallizing. At a halt the entire liquid phase crystallizes. So, what we would see as either of these mixtures is cooled would be a melting point range; the upper limit corresponding to the break (first appearance of a solid) and the lower limit corresponding to the halt (last drop of liquid solidifies).
Figure 2. Cooling curves corresponding to the isopleths shown in Fig. 1. Cooling curve 1 is for a mixture rich in compound A, while cooling curve 3 is for a mixture rich in compound B, and cooling curve 2 corresponds to a mixture with the eutectic composition. Note the small dip in temperature before each break and halt that indicates supercooling of the mixture; slow cooling should minimize this effect.
Obviously, a pure substance would have no breaks, as these are characteristic only of mixtures, and thus the cooling curve of a pure substance would consist of a single halt at a temperature corresponding to its melting point. The cooling curve along isopleth 2 is special in that it has no breaks, only a halt, at what is called the eutectic temperature. And a mixture that shows such behavior is said to have the eutectic composition. The point on a solid-liquid phase diagram corresponding to the eutectic temperature and eutectic composition is called the eutectic point.
It is also possible to go from a set of cooling curves to the corresponding phase diagram. If we were to collect a sufficient number of cooling curves and graph the temperatures at which the breaks as a function of composition, then we would generate the liquidus portion of the phase diagram. The halts, in turn, would define the eutectic temperature. From a fit of the two liquidus curves and a fit of the various eutectic temperatures, we would be able to define the eutectic composition from the mutual intersection of the lines.
While it is possible to perform these fits to empirical equations, it is more useful to derive actual equations that describe the liquidus curves, as this will allow us to extract more information from our data. We will assume that the systems under consideration do not form solid solutions, that is to say the components exists in their own separate pure phase in the solid state. In this way we can treat the system as simply one solid dissolving in one liquid. As long as the solutions are sufficiently dilute (i. e., behave ideally) we may use Eqn. 1 to relate the temperature at which crystallization occurs, T, to the mole fraction of the solute, χ. Also in Eqn. 1 are ΔfusH, the solute’s enthalpy of fusion, the solute’s melting point, T*, and the ideal gas constant, R. This equation may be already familiar to you from our discussion of colligative properties in lecture.
 |
(1) |
This equation may be solved for T to give the Schroder-van Laar equation, shown as Eqn. 2.
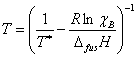 |
(2) |
While Eqn. 2 is not linear in χ, the curve fitting function of LoggerPro or the Solver function of Excel can be used to fit temperature as a function of mole fraction data to give T* and ΔfusH for each component of the mixture. For more information on binary solid-liquid phase diagrams and the derivation of these equations, please see the references.1-4
From your data, generate the solid-liquid phase diagram for your system and determine ΔfusH and the melting point for the two pure substances at 95% confidence. Determine the eutectic temperature and composition, along with your best estimate of the uncertainties for these values. Note that you will have to consider the data for compositions on either side of the eutectic composition separately. If your system behaves ideally, you may be able to use all of your data on either side of the eutectic in this analysis to determine ΔfusH and T* for each compound. However, if the system does behave ideally you will need more data for the dilute mixtures in order to determine ΔfusH and T*. It is advised that you attempt to fit your data between laboratory sessions to determine whether you have a sufficient number of points to complete your analysis with sufficiently high precision. Be sure to include your experimentally-derived phase diagram and example cooling curves in the results of your report. Compare your results to the literature.1 Are your results consistent with the literature within experimental uncertainty? Is the uncertainty in the mass or the temperature responsible for the uncertainties in your calculated quantities, or is some other factor responsible?
References
1. Gallus, J.; Lin, Q.; Zumbühl, A.; Friess, S. D.; Hartmann, R. and Meister, E. C. J. Chem. Educ. 2001, 78, 961-964. Click here for a PDF version of this article (Truman addresses and J. Chem. Educ. subscribers only).
2. Garland, C. W.; Nibler, J. W. and Shoemaker, D. P. Experiments in Physical Chemistry, 7th Ed.; McGraw-Hill: New York, 2003, p. 215-221.
3. Boardman, S. and Youngblood, L. J. Geol. Educ. 1975, 23, 52-54.
4. Atkins, P. and de Paula, J. Physical Chemistry, 8th Ed.; W. H. Freeman: New York, 2006, p. 189-193.
