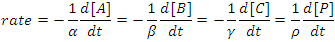Kinetics Review
Adapted from an Exercise developed by the Physical Chemists at the University of Kansas by J. M. McCormick
Last Update: January 17, 2012
The rate of a chemical reaction may be defined as either the rate of disappearance of the reactants or as the rate of appearance of the products. If we consider the rate of the generalized reaction αA + βB + γC → ρP, we may write
|
|
(1) |
Note the appearance of negative signs and stoichiometric coefficients in this equation. By defining the rate of reaction in this way the rate will always be a positive number that is independent of whether we follow a reactant or a product and that is independent of the overall balanced chemical equation.
Because we can control the amount of reactants present initially, it obvious that any equation that we would write to describe a reaction rate should involve the reactants (note that in some cases catalysts and products will appear in this equation, but we won’t concern ourselves with that situation, yet). This equation is known as the reaction’s rate law and is the fundamental equation of chemical kinetics. The rate law for the generalized reaction given above may be written in terms of the concentrations of the reactants (Eqn. 2), where k is the reaction’s rate constant and a, b and c are the orders of the reaction with respect to the reactants A, B and C, respectively. Generally, the order with respect to a chemical species is unrelated to its stoichiometric coefficient in the balanced chemical equation. Thus, the rate law cannot be deduced from a balanced chemical equation; it must be determined experimentally.
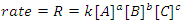 |
(2) |
There is only one exception to the general rule that one cannot write a rate law directly from a balanced chemical equation and this is for an elementary step in a reaction mechanism. Recall that a mechanism is a set of elementary steps that reflect the actual means by which a chemical reaction occurs. Since each elementary step represents an actual molecular event, its rate law may be written from its balanced chemical equation.
To be a possible mechanism for a chemical reaction a proposed mechanism’s elementary steps must sum to the overall balanced chemical equation for the reaction and the mechanism must predict a rate law that is consistent with the experimentally-determined rate law. While the construction of a mechanism is a fascinating subject in its own right, this web page will focus on ways to experimentally determine rate laws. The interested reader is referred to any physical chemistry or kinetics text for more information on this topic.1,2
The easiest kinetics cases to treat mathematically are those in which there is only one reactant, let’s let it be A, and only one step (thus, in the balanced chemical equation given above and Eqn. 2, b = c = β = γ = 0). Since there is only one step, we can write the rate law directly from the balanced equation and since there is only one reactant, we can simple integrate the resulting differential equation to obtain an equation that describes the concentration of A at any time, t (i. e., [A]t). There are three simple cases: the reaction is zeroth-order with respect to A (a = 0), the reaction is first-order with respect to A (a = 1), or the reaction is second-order with respect to A (a = 2). These three cases are referred to collectively as the integrated rate laws and are shown in Table 1 in their most common form. Note that there are a number of different ways to write these equations to take into account such things as a non-zero concentration at infinite time, that product formation is being monitored (i. e., [A]0 = 0), etc., and the interested reader is referred to specialized texts on kinetics for more information.1,2 The methods of Guggenheim and Job are of particular importance,2 but will not be discussed here.
Table 1. The integrated rate laws for zeroth, first and second order reactions.
To determine the order for a reaction with a single reactant, one only needs to prepare three graphs of the kinetics data, each according to the form of a different integrated rate law. From whichever graph gives the best fit to a straight line, one can directly deduce the order with respect to the reactant. One practical consideration in the use of the integrated rate laws is that data should be obtained for at least three half lives to differentiate between the three possiblities. This is because for sufficiently short times all three graphs can appear linear. It is tempting, in this age of computer-controlled spectrometers, to obtain more data, without extending the acquisition time, but this usually does not help to differentiate between the possible integrated rate laws. In addition, acquiring data at a rapid rate does not usually give more precise results, but just makes the data set harder to work with, and so is not recommended as a general course of action. There is one other experimental problem that is often encountered at long reaction times (after several half lives) where linear graphs will become decidedly non-linear. This is often the result of the assumptions that we’ve made to force a complex reaction to fit an integrated rate law (vide infra) or that subsequent, slower reactions are becoming important. Including these non-linear regions in a regression analysis may lead to incorrect results. Therefore, the experimentalist must graph his/her data as it is obtained and then critically analyze the results to optimize the method (not too many points, and not acquiring data much beyond three half lives, or wherever the data clearly become non-linear) so that the most precise and accurate results are obtained.
While there is a relatively simple integrated rate law for second order reactions involving two reactants,1 the simplest approach to determining a rate law with more than one reactant is to use the isolation method. In the isolation method the initial concentration of one of the reactants, let’s say B, whose initial concentration is [B]0, is much less than the initial concentrations of A, or C ([A]0 and [C]0, respectively). In this scenario, [A] and [C] will change only very little as the reaction proceeds, while B will be completely used up. It can then be assumed that the concentrations of A and C at any time, t, are equal to their initial values (i. e., [A]t = [A]0 and [C]t = [C]0, for all t). Since only [B] varies appreciably with time during the course of the reaction, Eqn. 2 can be rewritten as Eqn. 3, where R is the measured rate of reaction and the constant kAC equals k [A]0a[C]0c. The order with respect to B can then determined graphically using the integrated rate laws. Once the order with respect to B is known, the process is repeated by making the concentration of one of the other reactants small until the order of each reactant is found. The rate constant for the reaction is then found from any of the rate data.
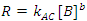 |
(3) |
In some cases, it is not possible to change the concentrations to satisfy the conditions set by the isolation method. For example, if we were following the reaction by monitoring the absorbance of species B, we would not be able to increase [B]0 without the absorbance being no longer proportional to the concentration (Beer’s Law fails). This would mean that we would not have an accurate measure of the [B]t and therefore the rate measurement would also be inaccurate. In this case, we are forced to fix [B]0 so that we can measure it, but we can still make systematic changes in the concentration of the other reactants, which are still much larger than that of B. If we hold [C]0 (and [B]0) constant, but vary [A]0 (note [A]0 > > [B]0), then the rate will change, if a reactant has a non-zero order. This is because the constantkAC changes (kAC = k [A]0a[C]0c, but we’ve changed [A]0!). We can obtain an equation that we can graph and fit to a straight line to extract the order with A by taking the logarithm of both sides of kAC = k [A]0a[C]0c to give Eqn. 4. In Eqn. 4 [A]0i is the initial concentration of A for a particular kinetics run, i, and kACi is the measured rate constant for that run (obtained using the integrated rate law that was used to find the order with respect to B). As long as we only change [A]0 (leaving [C]0 constant), a graph of logkACi as a function of [A]0i will be a straight line. If the order with respect to A is 0, then this graph is a horizontal line; otherwise it has slope of a (the order with respect to A) and an intercept ofk+clog[C]0i. If the order with respect to C is 0 (or there is no third reactant), then we would have been able to obtain the overall rate constant, k, from the graph of logkACi as a function of [A]0i. Once the order with respect to A is found, the process is repeated, but now varying C, to determine the order with respect to C. The value of the overall rate constant,k, would then be found from the intercepts and the known initial concentrations of A and C.
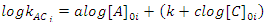 |
(4) |
There is a special case of this rate law when the rate of reaction is independent of the concentration of B (the order of the reaction with respect to B is 0; i. e., b = 0), but we are monitoring [B] as a function of time.3 In this case Eqn. 3 simplifies to Eqn. 5, which can be integrated to give Eqn. 6. So a graph of [B]t as a function of time will yield a straight line with an intercept of [B]0 and a slope of –kAC. As a check of whether the reaction is truly independent of B, the experiment can be repeated with different [B]0, keeping [A] and [C] constant, which should give graphs with the same slope, but with different intercepts.
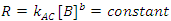 |
(5) |
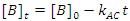 |
(6) |
In this case, where the order with respect to B is zero, one determines the order with respect to A and C by simply keeping [A]0 and [C]0 much greater than [B]0, and then systematically varying [A]0 and [C]0 in turn. For example, if we will hold [C]0 constant and vary [A]0, we will have i kinetics runs with initial concentrations of A in each run equal to [A]0i. Remembering that b equals 0 allows us to rewrite Eqn. 2 as Eqn. 7, where Ri is the rate of the ith run and kC is equal to k[C]0c. Thus, a graph of [B]t as a function of time for each run should give a straight line with a slope of –Ri, and Eqn. 7 predicts that the slopes of these lines (values of Ri) are proportional to [A]0a. To obtain a form of Eqn. 7 from which a can be extracted, one simply takes the logarithm of both sides of Eqn. 7 to give Eqn. 8. A graph of log Ri as a function of log[A]0i will give a straight line with a slope equal to a. This procedure is then repeated for reactant C ([B]0and [A]0 are kept constant while varying [C]0i) to give c.
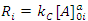 |
(7) |
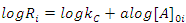 |
(8) |
There are, of course, many cases that can’t be treated using integrated rate laws or the simple methods given here. One can, for example, model a complex mechanism by solving the system of coupled differential equations, each of which describes how the concentration of a chemical species changes with time. Obviously, this method is both computer- and time-intensive and as such is not often encountered in an undergraduate teaching laboratory, but it is the only way to model complex systems such as the atmosphere or a living organism.
- 1. Atkins, P. and de Paula, J. Physical Chemistry, 8th Ed.; W. H. Freeman and Co.: New York, 2006; p. 791ff.
- 2. Laidler, K. J. Chemical Kinetics, 2nd Ed.; McGraw-Hill: New York, 1965.
- 3. Daniels, F.; Williams, J. W.; Bender, P.; Alberty, R. A. and Cornwell, C. D. Experimental Physical Chemistry, 6th Ed.; McGraw-Hill: New York, 1962; pp. 143-146.