The First Law and the Sign Convention used in Thermodynamics
Last Update: April 13, 2011
The version of the First Law of Thermodynamics with which you are probably most familiar is “energy can neither be created nor destroyed”. One mathematical statement of the First Law is given by Eqn. 1, where ΔU represents the change in a system’s internal energy (the combined kinetic and potential energies of the particles within the system), qis the heat that the system exchanges with its surroundings and w is the work done on, or by, the system.
|
ΔU = q + w |
(1) |
The system’s internal energy is a state function. This means that U is completely defined by the state variables of pressure (p), volume (V), temperature (T) and the amount of material in the system (n). It also means that upon going from one state (one set of state variables) to another state (a different set of state variables) the change in U (ΔU) depends only on the state variables in each state and not on how the system was taken from one state to another. For example, imagine a system that begins with state variables p1, V1, T1, n1. Let us then say that the system undergoes a number of processes that gives it a different set of state variables, but it is ultimately brought back to the original conditions (i. e., p1, V1, T1 and n1). No matter what was done to the system from beginning to end, the final internal energy of the system will be equivalent to its initial value (ΔU = 0).
In general it is not possible to determine a system’s total energy. However, it is possible to determine differences in a system’s internal energy as it undergoes a process going from one state to another. The mathematical version of the First Law makes clear that there will be no change in a system’s internal energy unless heat either leaves/enters the system and/or work is done by/on the system. By measuring how much heat leaves/enters a system and/or how much work is done by/on the system, one will be able to determine how much the internal energy of the system is changed.
The sign convention for designating whether thermal energy is leaving or entering a system is simple. Assuming no work is done, if heat leaves a system, the total energy content of the system decreases. Thus ΔU is negative and q is negative, and the process is said to be exothermic. In an endothermic process, heat enters a system causing the system’s total energy content to increases and so ΔU and q are positive. The sign conventions for work are similar, but require some explanation. The problem is that we need to clearly define what “work done by/on a system” means.
A constant force (F) applied through a displacement (Δd) gives work as given by Eqn. 2.
|
w = –F·Δd |
(2) |
There are a number of different types of work, including electrical work. However, the easiest to understand, and the relevant to our everyday experience is expansion work (also known as pressure-volume work), which is work associated with a system expanding or contracting against its surroundings. Under even moderate changes in pressure, the volumes of solids and liquids do not change appreciably and they are said to be virtually incompressible. And so, we will limit our discussion of expansion work to gases.
Consider a system consisting of a gas confined in a cylindrical container of cross-sectional area A, the volume of which is determined by the position of a weightless piston, as shown in Fig. 1. The particles of gas within the cylinder will exert a pressure, p, on the piston,
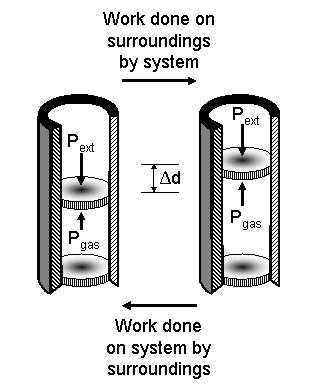Figure 1. Ideal thermodynamic system consisting of an ideal gas trapped in a cylindrical container separated from the constant pressure of the atmosphere (pext).
The particles of gas within the cylinder will exert a pressure, pgas, on the piston, which will be positioned such that the pressure of the gas is equal to a constant external pressure, pext. Pressure is defined to be a force applied to an area, so the force associated with the work done when the gas expands/contracts is given by Eqn. 3.
|
F = –pext·A |
(3) |
When the system of gas undergoes a change that would alter its pressure, the piston will move so that, once again, the pressures inside and outside the system are equivalent. Alternatively, the position of the piston may be forcibly changed, which would cause the gas to respond accordingly. A change in the position of the piston, Δd, causes a change in the volume of the gaseous system, and because volume is the product of height and cross-sectional area, the displacement associated with the work done when the gas expands/contracts can be written as Eqn. 4.
| (4) |
The expansion work done when the system undergoes a change can then be related to the change in volume, as shown in Eqn. 5
| (5) |
If work is done by the system, it pushes against the surroundings and expands. This means that ΔV is positive and thatw and ΔU are negative. In this case the system’s internal energy falls as some of its energy is transferred to the surroundings as work. If work is done on the system, the surroundings push against the system and it contracts. Now ΔV is negative, w is positive, and ΔU is positive, which means that energy is entering the system in the form of work done on it by its surroundings.
The difference in a system’s internal energy upon undergoing a chemical change (e. g., combustion of a hydrocarbon) can be directly measured by using a constant-volume calorimeter, or “bomb” calorimeter. The chemical reaction takes place in a heavy-walled container so that DV must equal zero. If no other work is done, then expansion work (w = –p·ΔV) must be zero, and by the First Law of Thermodynamics, the heat that the system exchanges with its surroundings is equal to ΔU directly (see Eqn. 6), where the “v” subscript on q reminds us that the heat was measured at constant volume.
| (6) |
For many reactions it is not convenient to use a bomb calorimeter to determine the changes in internal energy. Many chemical reactions take place at constant pressure. However, since pressure-volume work may be difficult to measure, it is convenient to measure enthalpies of reaction instead of changes in internal energy. Enthalpy (or “heat content”), represented by H, is defined to by Eqn. 7. Like internal energy, enthalpy is a state function.
|
H = U + p·V |
(7) |
Also like internal energy, it may not be possible to determine the enthalpy of a system at a particular state, but fortunately we are interested in the changes in enthalpy, ΔH, going from one state to another. If the pressure is constant (Δp = 0), the relationship between ΔH and ΔU can be written as Eqn. 8.
|
ΔH = ΔU + pΔV + VΔp = ΔU + pΔV + 0 = ΔU + pΔV |
(8) |
When only expansion work is considered, the change in internal energy is given by Eqn. 9, which when substituted into Eqn. 8 gives Eqn. 10, where the subscript “p” indicates that this heat is measured at constant pressure.
|
ΔU = q – pΔV |
(9) |
|
ΔH = (q – p·ΔV) + p·ΔV = qp |
(10) |