Determination of the Resonance Stabilization Energy
of Benzene by Bomb Calorimetry1,2
Adapted by J. M. McCormick
Last Update: August 23, 2013
Introduction
The structure and chemical reactivity of benzene was very puzzling to chemists for a number of years. They knew that it contained six carbon atoms and six hydrogen atoms, but not how the atoms were connected to give such a high degree of unsaturation. Kekulé famously solved the problem by postulating that benzene has a cyclic structure and three alternating double bonds. While this did explain some aspects of benzene’s properties and reactivity, it raised even more questions. These questions were eventually solved and lead to our modern picture of benzene. The simplest model of benzene’s structure has six pi electrons delocalized over the six carbon atoms giving six identical C-C bonds. For more details on the development of the resonance theory of benzene, the reader is directed to any introductory organic chemistry text.3 For a brief introduction to Kekulé’s life and work please see reference 4.4
One particularly important piece of evidence that lead to modification of Kekulé’s original theory, and eventually to our modern concept of resonance, was benzene’s anomalous enthalpy of hydrogenation (i. e., the heat released when a compound reacts with H2). Based on the enthalpy of hydrogenation of cyclohexene and 1,3-cyclohexadiene, the enthalpy of hydrogenation for 1,3,5-cyclohexatriene should be about -85.8 kcal/mole.3 However, benzene’s enthalpy of hydrogenation is significantly less exothermic than this, indicating that benzene’s structure is significantly more stable than the classic Kekulé structure. This difference in the enthalpy of hydrogenation is called the resonance stabilization energy (or more accurately a resonance stabilization enthalpy).
The resonance stabilization energy for benzene could be defined as the gas phase reaction of the hypothetical 1, 3, 5-cyclohexatriene to give benzene, as shown in Scheme 1. Unfortunately, cyclohexatriene does not exist (although we could create it using computational chemistry software) and therefore we cannot use this reaction to determine the resonance stabilization energy of benzene directly. However, it is possible to define the resonance stabilization energy of benzene in terms of a chemical reaction in the gaseous state between benzene and cyclohexane to give the compound trans, trans, cis-1, 5, 9-cyclododecatriene, CDDT, as shown in Scheme 2. Note that in Scheme 2 benzene has been shown to have a cyclohexatriene structure to emphasize that in this reaction the number and types of bonds do not change if benzene has the classic Kekulé structure. Since the number and types of bonds broken and formed are the same for the reaction, its enthalpy of reaction, DrH, should be zero. However, if benzene does not have a cyclohexatriene structure and its true structure is stabilized relative to 1, 3, 5-cyclohexatriene, then DrH, for this reaction will not be zero and will be equal to the resonance stabilization enthalpy of benzene (you can confirm this yourself by combining the reactions in Schemes 1 and 2 according to Hess’s Law).1,2
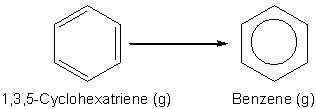
Scheme 1. The hypothetical reaction to form benzene from 1, 3,5-cyclohexatriene in the gaseous state that defines the resonance stabilization enthalpy of benzene.
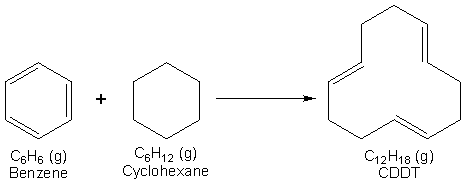
Scheme 2. An alternate reaction that can be used to define the resonance stabilization energy of benzene.
The advantage of the reaction in Scheme 2 is that all of the compounds exist and it is possible to construct a thermodynamic cycle using the enthalpies of combustion, DcombH, for each compound to determine DrH. The DcombH for liquid benzene and cyclohexane are known, as are their enthalpies of vaporization (DvapH), thus we only need to know the DcombH and DvapH for CDDT. The DvapH for CDDT may be calculated using the van’t Hoff equation from its vapor pressure, Pvap, which has been found by Rauh and coworkers to be described empirically by Eqn. 1,5 where the temperature, T, is in Kelvin. Thus, the only parameter left to be found is the DcombH of CDDT, which will be the goal of this exercise. More information on the theoretical background bomb calorimetry and the methods used are given in the literature,6-8 and online by clicking here.
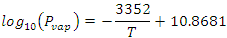 |
(1) |
Procedure
CAUTION! High pressures are used in this exercise and highly exothermic combustions are being studied. It is important that you exactly follow the instructions and follow all safety guidelines.1,6,9,10If you have any questions, ask your instructor.
You will be using a Parr 1341 plain jacket calorimeter and Parr model 1108 oxygen combustion bomb for your determination. IMPORTANT! You must be familiar with the operation of the calorimeter, the combustion bomb and the calorimetry thermometer before coming to the laboratory. CAUTION!Failure to follow the given procedures exactly may result in severe injury or death.
You will be using either the Parr 6772 calorimetry thermometer (Bomb Calorimeter 1) or the Parr 1661 calorimetry thermometer (Bomb Calorimeter 2) to record the temperature in the calorimeter as a function of time. Click on the appropriate link to view the operating instructions for the assigned thermometer. Note that each thermometer handles data output in a slightly different way, but whichever thermometer you use remember to save the data either to your Y: drive or a removable data storage device. LoggerPro has a number of useful features for manipulating and analyzing data, but all final figures should come from Excel. In either case, the acquisition parameters should be set initially so that data are recorded every 30 sec for 5 min before ignition and for 5 minutes after ignition.
The heat capacity of the calorimeter (also known as the calorimeter constant) will be determined by the combustion of benzoic acid (DcombH = +26.434 ± 0.003 kJ/g).6 You will need a pellet of benzoic acid weighing between 0.8 and 1.0 g with the weight known to the nearest 0.1 mg. Instructions on how to make a pellet of benzoic acid are given in the Parr 1341 calorimeter page. Helpful hint: the ratio of the temperature increase to the mass of benzoic acid used should agree within 1% for any two calibration runs.6 If they do not, then there is a serious problem with how the method is being executed.
To determine the DcombH for CDDT, approximately 0.7 g measured to the nearest 0.1 mg is delivered directly to the bomb’s combustion cup. CDDT has a sufficiently high boiling point that we do not need to worry about losing sample when filling the bomb with oxygen. However, care should be taken not to splash any CDDT out of the cup while handling the bomb. CAUTION! Use no more than the recommended amount of CDDT, and it is advised that you use no more than 80% of this amount for your first run. We have had one bomb failure while attempting the combustion of CDDT, and although we have not been able to identify the failure’s cause, it is recommended that care be taken when performing this reaction.
Once you have made an initial run with benzoic acid and one with CDDT, you should examine your data and re-evaluate the time intervals between each temperature measurement. You may be able to take less data, and therefore take less time to complete a measurement, but still maintain high precision in the results. At least two (preferably three) calibration runs must be done per day, and these should alternate with sample runs. It is advised that you start with a benzoic acid calibration run, then proceed to a CDDT sample run, and then another calibration run, etc. With proper planning and execution you should be able to perform six runs (3 samples, 3 standards) in a three-hour lab period.
Results and Analysis
Determine the heat given off by the reaction from the temperature change. From the benzoic acid runs, use the known DcombH for benzoic acid to determine the calorimeter constant. From the average value of the calorimeter constant (assuming that it was reproducible), calculate the heat given off by the combustion of CDDT. If your calorimeter constant varied from week to week, use the average calorimeter constant determined on a particular day in your calculations.
You will need to perform a number of corrections to the data before you can actually use it to determine the resonance stabilization energy of benzene. First, you will need to correct for any other reactions that took place in the bomb. To do this, we write a general equation (in Eqn. 2) for the measured heat released, qm, and its relationship to the actual heat released by the reaction, qact, the heat released by the combustion of the ignition wire, q1, and a term that corrects for the heat of reaction that accompanies the oxidation of N2 gas or other nitrogen sources in the bomb, q2. Since CDDT and benzoic acid do not contain nitrogen and the bomb should have been purged thoroughly before ignition, q2 is approximately equal to zero. The second term, q1, is important and may be calculated from the mass of wire burned and the energy released when the wire is burned (this relationship is given on the bomb wire package).
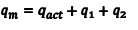 |
(2) |
Once the measured heat has been corrected for the burning of the ignition wire, you can compute the change in the internal energy of combustion, DcombU, for CDDT from the heat. This is DcombU because the reaction occurred under conditions of constant volume inside the bomb. Since we are interested in DcombH, you will need to convert the measured DcombU to DcombH before proceeding.8
Construct the thermodynamic cycle described in the Introduction needed to calculate the resonance stabilization enthalpy of benzene and include it in your final report. From your data, calculate the resonance stabilization enthalpy of benzene and report its value at 95% confidence. Compare your measured resonance stabilization energy with the generally accepted value(s). Propagate the uncertainties in the measured quantities through to the resonance stabilization energy of benzene. Identify what measured quantities contributed the most to the uncertainty in your final result.
1. Halpern, A. M. and McBane, G. C. Experimental Physical Chemistry, 3rd Ed.; W. H. Freeman: New York, 2006, p. 6.1-6.5.
2. Pickering, M. J. Chem. Educ. 1982, 59, 318. Click here to view as a PDF file (Truman addresses and J. Chem. Educ. subscribers only).
3. Solomons, T. W. G. Organic Chemistry, 4th Ed.; Wiley: New York, 1988, p. 487-504.
4. Lipeles, E. S. J. Chem. Educ. 1981, 58, 624-625. Click here to view as a PDF file (Truman addresses and J. Chem. Educ. subscribers only).
5. Rauh, H.-J.; Geyer, W.; Schmidt, H. and Geisler, G. Z. Phys. Chemie (Leipzig) 1973, 253, 43.
6. Halpern, A. M. and McBane, G. C. Experimental Physical Chemistry, 3rd Ed.; W. H. Freeman: New York, 2006, p. 5.1-5.15.
7. Garland, C. W.; Nibler, J. W. and Shoemaker, D. P. Experiments in Physical Chemistry, 8th Ed.; McGraw-Hill: New York, 2009, p. 145-158.
8. Atkins, P. and de Paula, J. Physical Chemistry, 8th Ed.; W. H. Freeman: New York, 2006, p. 37-56.
9. Parr Bulletin 1341, Plain Jacket Calorimeter; Parr Instrument Co.: Moline, IL, 1977.
10. Wilson, L. Y. and Tatum, R. J. Chem. Educ. 1985, 62, 902. Click here to view as a PDF file (Truman addresses and J. Chem. Educ. subscribers only).
